[ Get the code at github ]
A programming language is low level when its programs require attention to the irrelevant. Quote: – Alan J. Perlis
It’s not only that physicists can’t program (we rarely use version control, we don’t plan, we don’t test… I suppose most labs score zero on The Joel Test). It is that we program, we program a lot and we still mostly use Fortran!
Now I’m not implying that Fortran is not a good language. Fortran is just fine. What I’m saying is that Fortran is a very bad choice for non-programmers who do a lot of programming.
Over the years some have turned to other languages like C, C++ and Matlab. Some, perhaps more enlightened, have even turned to Python. Naturally, I, too, turned to other languages and soon began wondering about what else might be out there (language-wise) to help a poor physicist do his job.
Could there be a language that won’t break everything apart just because a number is consider “special”? (What’s a float or a double? Why do I care?) Could there be one that implements a few-lines-of-equations-model in a few lines of code? One that will help me in my work not make the problem just … different?
I’ve been googling and poking around on stackoverflow and programmers.SE for some answers but nothing particularly interesting came up. It, thus, seems that I have to try them all.
- “Rules”
-
no extra packages
-
idiomatic code for each language
-
efficiency is not so much of an issue
-
extendable code
The system
I’ll be solving, as an example, the following 2D system of ordinary differential equations:
$$ \begin{aligned} \frac{df_1(x)}{dx} =& 1 - f_2(x)\\ \frac{df_2(x)}{dx} =& f_1(x) - x \end{aligned} $$
with initial conditions:
$$\begin{aligned} x_0 &= 0\\ f_1(x_0) &= 1\\ f_2(x_0) &= 0 \end{aligned}$$
in the range $$[0, 3]$$
The exact solution is $$\begin{aligned} f_1(x)&=\cos{x}+x\\ f_2(x)&=\sin{x}\end{aligned}$$
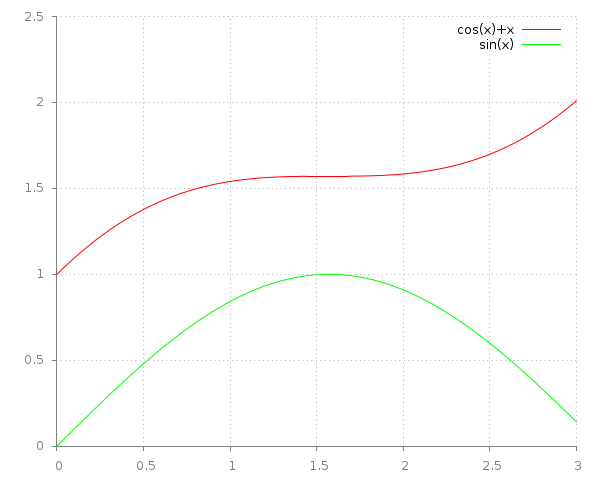
To numerically solve the system we treat the function values $$f_i(x)$$ as parameters of the differential functions:
$$ \begin{aligned} F_1(x,y_1,y_2) &= \frac{df_1(x,y_1,y_2)}{dx} =& 1 - y_2\\ F_2(x,y_1,y_2) &= \frac{df_2(x,y_1,y_2)}{dx} =& y_1 - x \end{aligned} $$
We will end up with a list of \(y_{i,0},\ldots,y_{i,n}\) values that will represent an approximation of the values \(f_i(x_k),\, x_k = x + k\cdot\delta x\).
The method: Runge Kutta-4
Runge Kutta method iterates from a current known value of $$f(x)$$ to the “next” value at $$x+\delta x$$. So, knowing $$f(x_0)$$ and choosing a small step $$\delta x$$ the method gives us $$f(x_0 + \delta x)$$ by calculating a “correction” to $$f(x_0)$$.
We thus have: $$ f(x_0 + \delta x) = f(x_0) + \Delta()$$ where the correction $$\Delta()$$ depends on $$\delta x, x_0, f(x_0), f\prime(x,y)$$ and is given by:
$$ \Delta(\delta x, x_0, f(x_0), f\prime(x,y)) = \frac{1}{6}\delta x (a + 2b + 2c + d) $$
where
$$ \begin{aligned} a = & f\prime(x_0, f(x_0))\\ b = & f\prime(x_0 + \frac{1}{2}\delta x, f(x_0) + \frac{1}{2}a\delta x)\\ c = & f\prime(x_0 + \frac{1}{2}\delta x, f(x_0) + \frac{1}{2}b\delta x)\\ d = & f\prime(x_0 + \delta x, f(x_0) + c\delta x) \end{aligned} $$
We feed $$\Delta()$$ with the initial known values.
In many dimensions
To apply RK4 to a system of ODEs
for each set of equations $$F_i = f_i\prime(x_0, y_1, \ldots, y_n)$$ we have a different set of parameters $$a_i, b_i, c_i, d_i$$ and a correction function $$f_i(x_0 + \delta x) = f_i(x_0) + \Delta(\delta x, a_i,b_i,c_i,d_i) $$
$$\begin{aligned} a_i &= F_i(x_0 ,& y_1,& \ldots ,& y_n) \\ b_i &= F_i(x_0+\frac{1}{2}\delta x ,& y_1 + \frac{1}{2}a_1\delta x ,& \ldots ,& y_n + \frac{1}{2}a_n\delta x)\\ c_i &= F_i(x_0+\frac{1}{2}\delta x ,& y_1 + \frac{1}{2}b_1\delta x ,& \ldots ,& y_n + \frac{1}{2}b_n\delta x)\\ d_i &= F_i(x_0+\delta x ,& y_1 + c_1\delta x ,& \ldots ,& y_n + c_n\delta x)\\ \end{aligned}$$
$$ \Delta() = \frac{1}{6}\delta x (a_i + 2 b_i + 2 c_i + d) $$
$$ f_i(x_0 + \delta x) = f_i(x_0) + \Delta(\delta x, a_i,b_i,c_i,d_i) $$
The Code
I’ll use a C implementation as a reference.
C (reference)
Adapted from numerical recipes in C:
void rk4(double y[], double dydx[], int n, double x, double h, double yout[], void (*derivs)(double, double [], double []))
{
int i;
double xh, hh, h6;
double dym[n], dyt[n], yt[n];
hh = h*0.5;
h6 = h/6.0;
xh = x+hh;
for (i=0;i<n;i++) yt[i] = y[i] + hh*dydx[i];
(*derivs)(xh,yt,dyt);
for (i=0;i<n;i++) yt[i] = y[i] + hh*dyt[i];
(*derivs)(xh,yt,dym);
for (i=0;i<n;i++) {
yt[i] = y[i] + h*dym[i];
dym[i] = dym[i] + dyt[i];
}
(*derivs)(x+h,yt,dyt);
for (i=0;i<n;i++)
yout[i] = y[i] + h6*(dydx[i] + dyt[i] + 2.*dym[i]);
}
void rkdump(double vstart[], int nvar, double t1, double t2, int nstep, void (*derivs)(double, double[], double[]))
{
int i,k;
double x,h;
double v[nvar], vout[nvar], dv[nvar];
for (i=0;i<nvar;i++) {
v[i] = vstart[i];
}
x = t1;
h = (t2-t1)/nstep;
for (k=0;k<nstep;k++) {
(*derivs)(x,v,dv);
rk4(v,dv,nvar,x,h,vout,derivs);
if ((double)(x+h) == x) printf("Step size too small in routine rkdump\n");
x += h;
for (i=0;i<nvar;i++) {
v[i] = vout[i];
}
solution[0][k] = v[0];
solution[1][k] = v[1];
}
}
for example:
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <complex.h>
#define N 2 //Dimensions
#define x0 0.0
#define x1 3.0
#define dt 0.01
double *solution[N] = {NULL};
void deriv1 (double x, double y[], double dydt[])
{
dydt[0] = 1 - y[1];
dydt[1] = y[0] - x;
}
int main (void)
{
int i;
int steps; // solution steps
double starting_v[N]; // Starting vector
steps = (x1-x0)/dt;
for (i=0;i<N;i++)
solution[i] = (double *)realloc((char *)solution[i], sizeof(double)*steps);
/* -- initial values -- */
starting_v[0] = 1.0;
starting_v[1] = 0.0;
rkdump(starting_v, N, x0, x1, steps, deriv1);
for (i=0;i<steps;i++) {
printf("%4f %4f %4f\n", (i+1)*dt, solution[0][i], solution[1][i]);
}
return 0;
}
Coming up: J, LISP, R, Fortran, Python, Haskell, Pari/GP, maxima.
Any other languages that you would like to see?